Gears

Gears are machine elements that transmit motion by means of successively engaging teeth. The gear teeth act like small levers.

1 Gear Classification

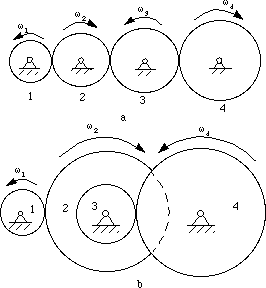
Gears may be classified according to the relative position of the axes of revolution. The axes may be

1. parallel,
2. intersecting,
3. neither parallel nor intersecting.

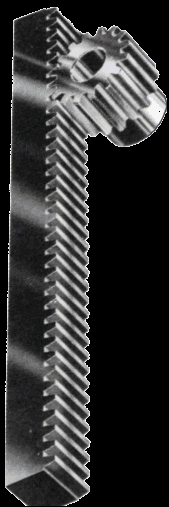
Gears for connecting parallel shafts

1. Spur gears   

   The left pair of gears makes external contact, and the right pair of gears makes internal contact

    

2. Parallel helical gears
3. Herringbone gears (or double-helical gears)
4. Rack and pinion (The rack is like a gear whose axis is at infinity.)

Gears for connecting intersecting shafts

1. Straight bevel gears
2. Spiral bevel gears

Neither parallel nor intersecting shafts

1. Crossed-helical gears
2. Hypoid gears
3. Worm and wormgear

2 Gear-Tooth Action

2.1 Fundamental Law of Gear-Tooth Action

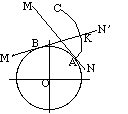
Figure 1 shows two mating gear teeth,

Figure 1 Two gearing tooth profiles

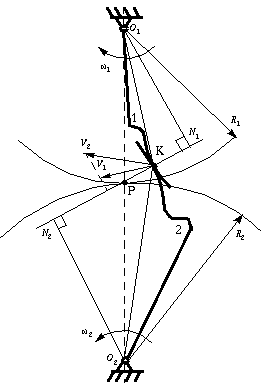
Although the two profiles have different velocities V₁ and V₂ at point K, their velocities along N₁N₂ are equal in both magnitude and direction. Otherwise the two tooth profiles would separate from each other.

Point P is very important to the velocity ratio, and it is called the pitch point. Pitch point divides the line between the line of centers and its position decides the velocity ratio of the two teeth. The above expression is the fundamental law of gear-tooth action.

2.2 Constant Velocity Ratio

For a constant velocity ratio, the position of P should remain unchanged. In this case, the motion transmission between two gears is equivalent to the motion transmission between two imagined slipless cylinders with radius R₁ and R₂ or diameter D₁ and D₂. We can get two circles whose centers are at O₁ and O₂, and through pitch point P. These two circle are termed pitch circles. The velocity ratio is equal to the inverse ratio of the diameters of pitch circles. This is the fundamental law of gear-tooth action.

The fundamental law of gear-tooth action may now also be stated as follow (for gears with fixed center distance):

The common normal to the tooth profiles at the point of contact must always pass through a fixed point (the pitch point) on the line of centers (to get a constant velocity ration).

2.3 Conjugate Profiles

To obtain the expected velocity ratio of two tooth profiles, the normal line of their profiles must pass through the corresponding pitch point, which is decided by the velocity ratio. The two profiles which satisfy this requirement are called conjugate profiles. Sometimes, we simply termed the tooth profiles which satisfy the fundamental law of gear-tooth action the conjugate profiles.

Although many tooth shapes are possible for which a mating tooth could be designed to satisfy the fundamental law, only two are in general use: the cycloidal and involute profiles. The involute has important advantages -- it is easy to manufacture and the center distance between a pair of involute gears can be varied without changing the velocity ratio. Thus close tolerances between shaft locations are not required when using the involute profile. The most commonly used conjugate tooth curve is the involute curve 

3 Involute Curve

The following examples are involute spur gears. We use the word involute because the contour of gear teeth curves inward. Gears have many terminologies, parameters and principles. One of the important concepts is the velocity ratio, which is the ratio of the rotary velocity of the driver gear to that of the driven gears.

3.1 Generation of the Involute Curve

Figure 2 Involute curve

The curve most commonly used for gear-tooth profiles is the involute of a circle. This involute curve is the path traced by a point on a line as the line rolls without slipping on the circumference of a circle. It may also be defined as a path traced by the end of a string which is originally wrapped on a circle when the string is unwrapped from the circle. The circle from which the involute is derived is called the base circle.

4 Terminology for Spur Gears

Figure 3 shows some of the terms for gears.

Figure 3 Spur Gear

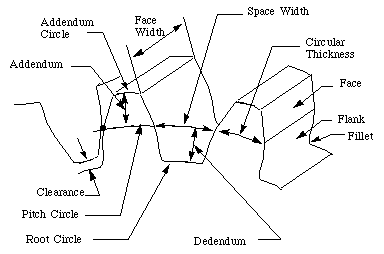
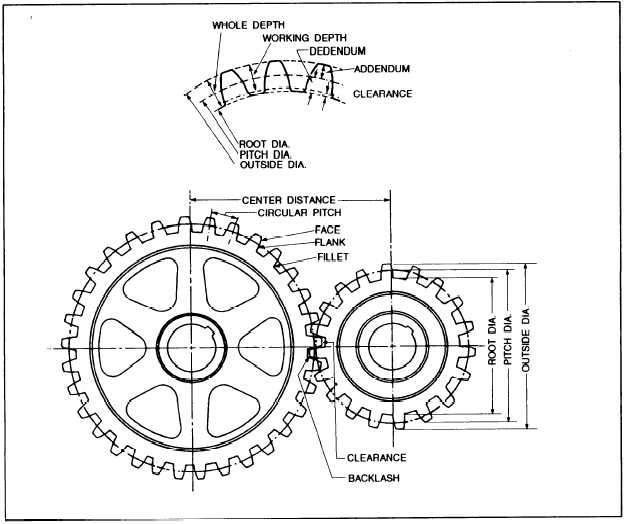
In the following section, we define many of the terms used in the analysis of spur gears. Some of the terminology has been defined previously but we include them here for completeness.

• Pitch surface : The surface of the imaginary rolling cylinder (cone, etc.) that the toothed gear may be considered to replace.
• Pitch circle: A right section of the pitch surface.
• Addendum circle: A circle bounding the ends of the teeth, in a right section of the gear.
• Root (or dedendum) circle: The circle bounding the spaces between the teeth, in a right section of the gear.
• Addendum: The radial distance between the pitch circle and the addendum circle.
• Dedendum: The radial distance between the pitch circle and the root circle.
• Clearance: The difference between the dedendum of one gear and the addendum of the mating gear.
• Face of a tooth: That part of the tooth surface lying outside the pitch surface.
• Flank of a tooth: The part of the tooth surface lying inside the pitch surface.
• Circular thickness (also called the tooth thickness) : The thickness of the tooth measured on the pitch circle. It is the length of an arc and not the length of a straight line.
• Tooth space: The distance between adjacent teeth measured on the pitch circle.
• Backlash: The difference between the circle thickness of one gear and the tooth space of the mating gear.
• Circular pitch p: The width of a tooth and a space, measured on the pitch circle.
• Diametral pitch P: The number of teeth of a gear per inch of its pitch diameter. A toothed gear must have an integral number of teeth. The circular pitch, therefore, equals the pitch circumference divided by the number of teeth. The diametral pitch is, by definition, the number of teeth divided by the pitch diameter. That is,

  and

  

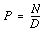
  Hence

  

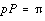
  where

  p = circular pitch

  P = diametral pitch

  N = number of teeth

  D = pitch diameter

  That is, the product of the diametral pitch and the circular pitch equals .

   

• Module m: Pitch diameter divided by number of teeth. The pitch diameter is usually specified in inches or millimeters; in the former case the module is the inverse of diametral pitch.
• Fillet : The small radius that connects the profile of a tooth to the root circle.
• Pinion: The smaller of any pair of mating gears. The larger of the pair is called simply the gear.
• Velocity ratio: The ratio of the number of revolutions of the driving (or input) gear to the number of revolutions of the driven (or output) gear, in a unit of time.
• Pitch point: The point of tangency of the pitch circles of a pair of mating gears.
• Common tangent: The line tangent to the pitch circle at the pitch point.
• Line of action: A line normal to a pair of mating tooth profiles at their point of contact.
• Path of contact: The path traced by the contact point of a pair of tooth profiles.
• Pressure angle : The angle between the common normal at the point of tooth contact and the common tangent to the pitch circles. It is also the angle between the line of action and the common tangent.
• Base circle :An imaginary circle used in involute gearing to generate the involutes that form the tooth profiles.

Table lists the commonly used diametral pitches.

5 Condition for Correct Meshing

Figure 4 shows two meshing gears contacting at point K₁ and K₂.

Figure 4 Two meshing gears

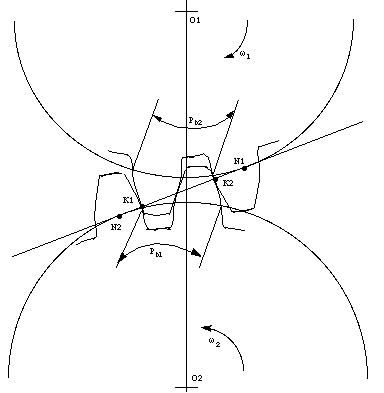
To get a correct meshing, the distance of K₁K₂ on gear 1 should be the same as the distance of K₁K₂ on gear 2. As K₁K₂ on both gears are equal to the base pitch of their gears, respectively.

6 Ordinary Gear Trains

Figure 5 Ordinary gear trains

7 Planetary gear trains

Figure 6 Planetary gear trains